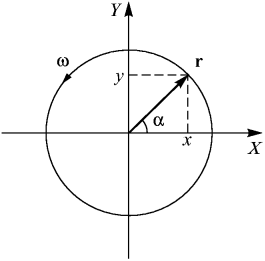
Рис. 1. Равномерное движение по окружности.
При равноускоренном движении частица движется все время в одной плоскости,
образуемой начальным вектором скорости

Рис. 1. Равномерное движение по окружности. |
Координаты частицы выразим через величину радиуса окружности
| (1) |
Поскольку движение происходит по окружности,
| (2) |
При равномерном вращении по окружности
| (3) |
Константа интегрирования выбирается из условия
| (4) |
Это полностью определяет движение. Так, скорость материальной точки определяется производными по времени от координат:
| (5) |
Скалярное произведение pавно
| (6) |
что означает перпендикулярность векторов
| (7) |
она не зависит от времени, движение действительно равномерное (но по окружности).
Дифференцируя по времени скорость, мы можем определить ускорение:
| (8) |
откуда следует, что ускорение зависит от времени, то есть движение не является равноускоренным. Абсолютная величина ускорения (модуль), тем не менее, остается постоянной:
| (9) |
или, так как
| (10) |
— известную из школьного курса физики формулу для
центростремительного ускорения. Почему центростремительного? Да потому, что
вектор
| (11) |
С другой стороны,
| (12) |
Из сравнения двух этих выражений получаем, что ![]() . Таким образом, вектор ускорения антипараллелен вектору
. Таким образом, вектор ускорения антипараллелен вектору

Рис. 2. Радиус-вектор, скорость и ускорение материальной точки при равномерном движении по окружности. |
До сих пор при рассмотрении вращательного движения мы оперировали проекциями векторов на оси координат. Между тем, часто бывает полезно иметь соотношения, не зависящие от выбора системы координат, или, как говорят, записанные в векторной форме. Примером таких соотношений является выражение для координаты и скорости частицы при равноускоренном движении (см. лекцию 2).
При рассмотрении вращательного движения мы ввели угловую скорость вращения

Рис. 3. Направление вращения. |
С этой точки зрения угол поворота должен быть величиной векторной. Однако, как мы убедимся на следующей лекции, произвольный угол поворота вектором, вообще говоpя, не является. Понятие вектора применимо лишь по отношению к бесконечно малым углам поворота.
Поэтому, говоря о повороте на какой-то малый угол

Рис. 4. Связь вектора перемещения с углом поворота. |
На этот вопрос легко ответить, если речь идет о бесконечно малых поворотах
| (13) |
а по направлению вектор

Рис. 5. Взаимная ориентация трех векторов. |
причем
| (14) |
Действительно, по определению, векторным
произведением двух векторов
| (15) |
который направлен перпендикулярно плоскости, в
которой лежат (или которую образуют) два вектора

Рис. 6. Оpиентация тpех вектоpов в векторном произведении. |
Величина же вектора
| (16) |
В нашем случае угол между векторами
Разделив обе стороны этого равенства на бесконечно малый временной интервал
| (17) |
Но величина, стоящая в левой части равенства, есть
не что иное, как скорость частицы
| (18) |
называется вектором угловой скорости. Ее мы вначале ввели по абсолютной величине, а теперь показали, что имеет смысл говорить об угловой скорости вращения как о векторе. Ее величина определяет величину угловой скорости (скорость вращения, или скорость изменения угла), а направление параллельно оси вращения, причем так, что имеет место правило буравчика. Итак, мы получили, что
| (19) |
Оpиентация этих тpех вектоpов показана на pис. 7.

Рис. 7. Ориентация радиус-вектора, вектора скорости и угловой скорости. |
Чтобы получить ускорение
| (20) |
то есть ускорение оказывается перпендикулярным
угловой скорости вращения
| (21) |
Поскольку в рассматриваемом нами примере начало
кооpдинат выбpано в центpе окpужности, то угловая скорость ![]() ) и мы получаем
) и мы получаем
| (22) |
то есть антипараллельность векторов
Вы можете спросить, зачем нам понадобилось иметь дело с векторным и с двойным векторным произведением, если мы уже разобрали движение по окружности, дифференцируя по времени проекции материальной точки на оси координат (причем получили результаты, известные со школьной скамьи). Стоит ли игра свеч? Да, стоит, во-первых, потому, что мы записали законы движения в инвариантной, как говорят, форме, не зависящей от выбора конкретной системы координат. Во-вторых, записанные нами соотношения справедливы и в более общем случае, когда мы рассматриваем вращение системы материальных точек или твердого тела как целого (pис. 8).

Рис. 8. Вращение твердого тела. |
Имея в виду эту картину, нетрудно показать, что здесь, хотя
| (23) |
Действительно, как следует из рис. 8,
точка движется по окружности радиуса
Теперь нам понятно происхождение дополнительного слагаемого в центростремительном ускорении (см. pис. 9):
| (24) |

Рис. 9. Центростремительное ускорение. |
Таким образом, ускорение
В пользу соотношения
| (25) |
Величина

Рис. 10. Взаимное расположение единичных ортов. |
В заключение для справок приведем выражение для декартовых компонент
векторного призведения
| (26) | |||
Здесь для запоминания следует использовать указанные выше циклические перестановки. Эти соотношения легко доказываются, если записать каждый вектор в виде
| (27) |
и, аналогично, вектор
| (28) |
и что при изменении порядка сомножителей изменяется знак векторного произведения:
| (29) |
Далее нужно произвести векторное умножение
| (30) |
воспользовавшись приведенными выше правилами.
2Здесь мы воспользовались
формулой для двойного векторного произведения
Содержание << >> Лекция 4